"Variance-Covariance matrix" unnecessarily redundant

Stop saying "variance-covariance matrix." It's just "covariance matrix."

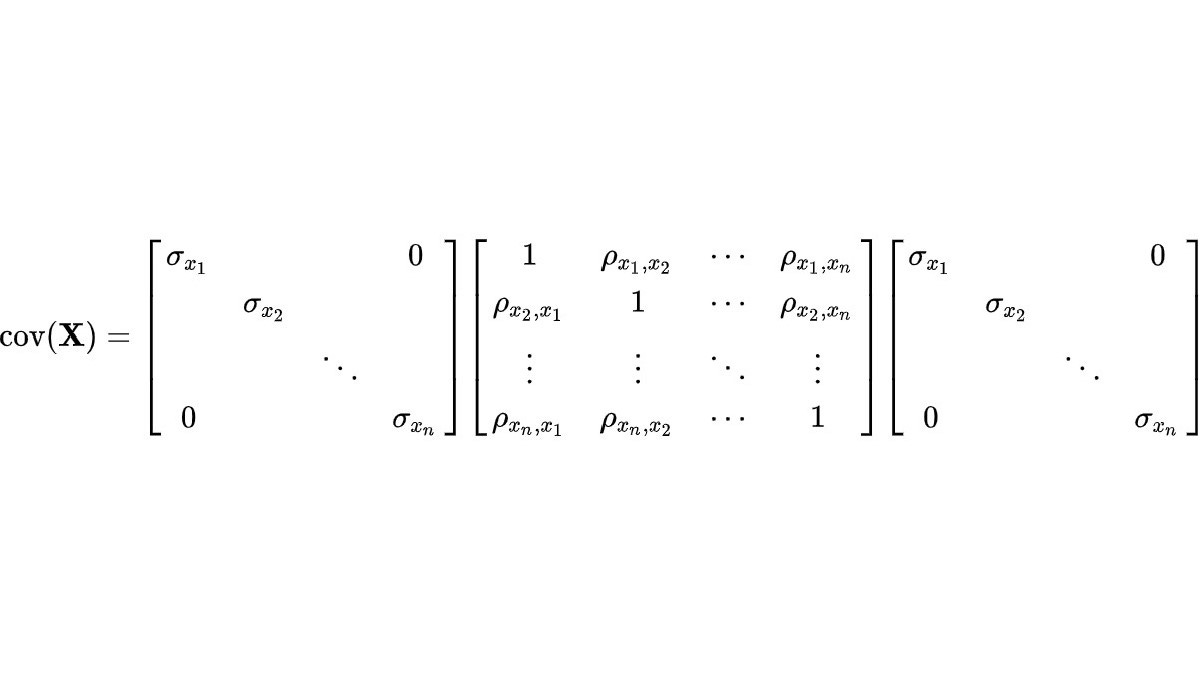
A covariance matrix is a symmetric matrix in which each element i,j = covariance(X_i, X_j), where X_i is a random variable. By definition the diagonal elements i,i = covariance(X_i, X_i) ≡ variance(X_i). That is always true of a covariance matrix, so there is no need to (re-)state that. I.e., adding the prefix "variance-" to the term "covariance matrix" never adds information. Except, perhaps, to suggest that the speaker does not fully understand this.

(I've heard some suggest that referring to it as a "variance-covariance" matrix helpfully reminds people that the diagonal is the variance of each variable. But if the reader or writer doesn't already understand that then they're not going to get very far with the topic.)